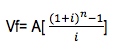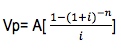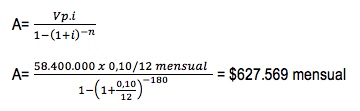Anualidades: ¿sabe qué son y cómo calcularlas?
Las anualidades son pagos periódicos iguales que no necesariamente tienen que ser anuales como lo indica su nombre; un ejemplo de este tipo de pagos son las pensiones, seguros, deudas pactadas con abonos iguales, etc.

Las anualidades son pagos periódicos iguales que no necesariamente tienen que ser anuales como lo indica su nombre; un ejemplo de este tipo de pagos son las pensiones, seguros, deudas pactadas con abonos iguales, etc.
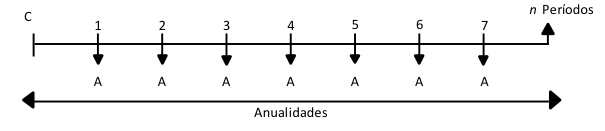
Las anualidades se caracterizan por ser una sucesión de pagos, generalmente iguales que se proyectan en períodos constantes de tiempo. A pesar de su nombre, las anualidades no implican la obligatoriedad de establecimiento de rentas anuales; por el contrario, solo se hace referencia a una secuencia de pagos con características constantes (iguales en todos los casos) y con intervalos de tiempo regulares, como se ejemplifica en la siguiente gráfica:
Como se ha comentado en anteriores editoriales de la línea de finanzas, a la hora de realizar la planeación presupuestal y la proyección financiera de las organizaciones, suele ser de mucha importancia tener en cuenta conceptos como el del valor del dinero en el tiempo y la premisa de que desde el punto de vista financiero, no es lo mismo pagar parcialmente, bien sea antes o después de cada período transcurrido, que haberlos pagado al final del vencimiento; esto en razón de que al recibir o pagar en una u otra fecha, se gana o se pierde la posibilidad de invertir los recursos en proyectos de mayor rendimiento; de ahí la importancia de poder calcular anualidades, pues para realizar la correcta programación de pagos periódicos iguales, deben tenerse en cuenta todas estas variables.
En esta ocasión, es importante afianzar conceptos para conocer a qué valor presente o futuro equivale una anualidad; y en sentido contrario, una anualidad a qué valor presente o futuro equivale. De ese modo los cálculos aquí presentados le permitirán, a las compañías que lo requieran, calcular por ejemplo el valor de las cuotas iguales que deben pagar por una nueva oficina o bodega adquirida con un plan de financiación o el valor acumulado de sus depósitos si periódicamente consigna el mismo valor.
Los siguientes son conceptos y parámetros que deben tenerse en cuenta para entender el modelo de cálculo de anualidades:
- Renta: valor nominal de cada pago periódico.
- Período de pago de renta: tiempo fijado entre dos pagos sucesivos.
- Plazo de la anualidad: tiempo que transcurre desde el inicio del primer pago y el final del último.
- Tasa de la anualidad: tasa de interés fijada en la operación financiera.
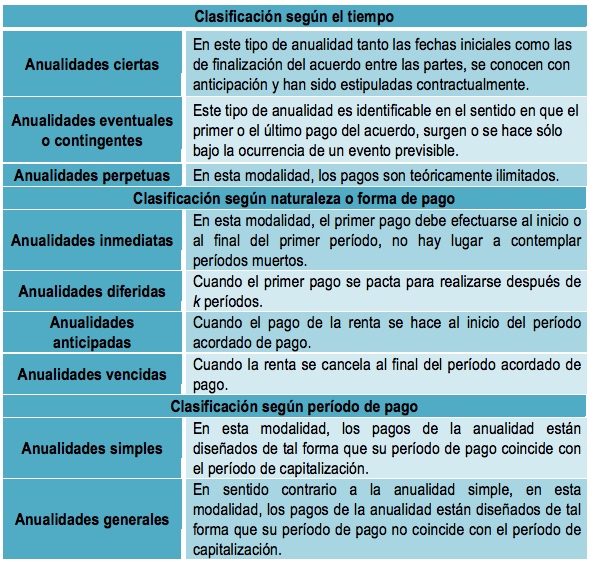
Adicionalmente, debe tenerse en cuenta que las anualidades pueden clasificarse en tres categorías: la primera, está diseñada con base en el criterio del tiempo; la segunda, el criterio es la naturaleza o forma de pago; y la tercera es la establecida de acuerdo con el período de pago, como se indican a continuación:
Actualmente, el cálculo de anualidades simples ya cuenta con modelos matemáticos para su cálculo, como lo es:
A= renta o pago periódico
J= tasa nominal anual
i= tasa efectiva por período de capitalización
m= número de períodos capitalizables en un año
n= número de períodos de pago
Vf= monto o valor de la anualidad
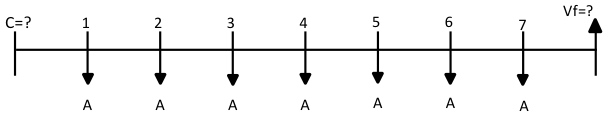
Valor futuro para anualidades simples vencidas
Valor presente para anualidades simple vencidas
Veamos un ejemplo:
La empresa XYZ desea vender una de sus bodegas que actualmente está en desuso por $73.000.000; en la mejor propuesta de los compradores ofertantes se propone pagar una cuota inicial del 20% y un pago diferido fijo a 15 años con una tasa de interés del 10% nominal anual capitalizable mensualmente ¿cuál debería ser el valor de las cuotas mensuales que debe acordar la compañía XYZ con su comprador?
Cuota inicial: $73.000.000 x 20% = $14.600.000
Deuda: $58.400.000
Este es el caso de una anualidad simple en la que se conoce con anticipación el valor presente de la deuda, por tal razón el cálculo correcto debe partir de convertir la fórmula de valor presente para anualidades simples vencidas, despejando A, para obtener: