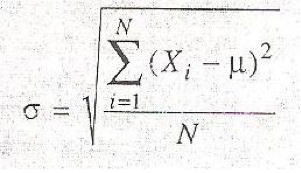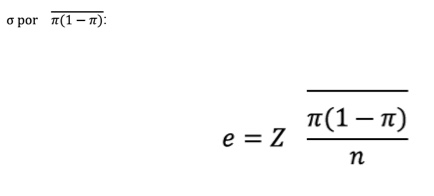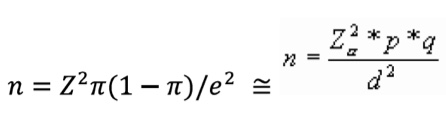Determinación del tamaño de una muestra en auditoría
De acuerdo con las Normas Internacionales de Auditoría, el profesional que revisa la información financiera de una entidad puede seleccionar una muestra utilizando algún método estadístico o acudiendo a su criterio profesional. En este editorial recordamos una forma matemática para hacerlo.

De acuerdo con las Normas Internacionales de Auditoría, el profesional que revisa la información financiera de una entidad puede seleccionar una muestra utilizando algún método estadístico o acudiendo a su criterio profesional. En este editorial recordamos una forma matemática para hacerlo.
Al seleccionar muestras para la aplicación de pruebas de auditoría es preciso tener en cuenta los criterios de tiempo y el presupuesto, por tanto, las habilidades del auditor o revisor para hacer una correcta selección de información son una ventaja importante en el momento de ejecutar la revisión. Para tal finalidad, la estadística aporta sencillas herramientas como las presentadas a continuación.
Determinación del tamaño de la muestra para la media
En este subtítulo aprenderemos a determinar el tamaño de la muestra necesario para estimar la media poblacional; para poder llevar a cabo este procedimiento, debemos conocer los siguientes datos:
1. El nivel de confianza, que determina el valor de Z o valor crítico de la distribución normal estandarizada.
2. El error de muestreo aceptable (e)
3. la desviación estándar (σ)
La desviación estándar puede ser calculada con la fórmula:
Donde μ es la media poblacional, que es la suma de los valores de la población dividida por el tamaño de la población N.
Sin embargo, en el entorno de los negocios, los contratos legales especifican el nivel de confianza requerido y el nivel de error más alto aceptado, dependiendo del sector en donde se esté. Como lo aclaran Levine, Krehbiel y Berenson en Estadística para Administración: “las regulaciones gubernamentales a menudo especifican los errores de muestreo y los niveles de confianza… por lo general, sólo un experto en la materia (es decir, el individuo más familiarizado con las variables estudiadas) es quien establece dichos datos” (Pág. 254). Cabe aclarar que, si bien ninguna empresa desea tener errores, debe tener claro cuánto es el máximo nivel de error que está dispuesta a tolerar, por lo cual los niveles de confianza más usados, según dichos autores, son el 95% y el 99%.
Veamos un caso: La empresa “El ejemplo S.A.S” proveedora de servicios de internet, desea conocer el promedio de horas semanales que sus clientes acceden a tal producto, a fin de estimar un promedio mensualizado sobre el que proyectar paquetes de ofertas y aumentar las ventas. La muestra será extraída de una población de 10.000 clientes que figuran en las bases de datos del área de recaudo y a los cuales se conoce a través de un estudio piloto, cuya desviación estándar es 3,11.
Si el comité de control interno de la compañía determinó un nivel de confianza de 0,95 y se plantea estar dispuesto a admitir un error máximo de 0,1, ¿cuál debe ser el tamaño maestral a emplear para el estudio?
Buscamos en las tablas de áreas bajo de la curva de una distribución normal el valor de 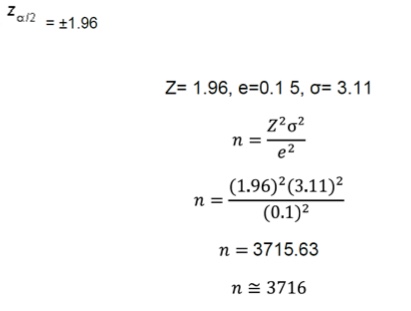
Redondeando al número entero más próximo; se sugiere que la compañía elija una muestra de 3.716 clientes a entrevistar.
Determinación del tamaño de la muestra para la proporción
En este apartado se aprenderá a determinar el tamaño de la muestra necesario para estimar la proporción; para poder efectuar dicha tarea, debemos conocer los siguientes datos:
1. El nivel de confianza, el cual determina el valor de Z o valor crítico de la distribución normal estandarizada.
2. El error de muestreo aceptable (e)
3. La proporción poblacional π
El error de muestreo, que indica la cantidad de error que se está dispuesto a tolerar, debe calcularse usando la variable π; para calcular el error de muestreo cuando se estima una proporción, debemos reemplazar
Sin embargo π es en realidad el parámetro poblacional que deseamos estimar: ¿cómo se establece un valor para el mismo objeto del que estamos tomando una muestra para poder determinarlo?
Pues bien, los autores de Estadística para Administración plantean dos posibles soluciones: una de ellas es trabajar con base en sucesos pasados e información previa que nos permita calcular el valor de π sin subestimar el tamaño realmente necesario de la muestra.
La otra opción es trabajar con el valor de π que haga la cantidad ![]() lo más grande posible. Por esta razón, cuando no se tiene conocimiento previo o una estimación de la proporción poblacional π, debemos utilizar π =0.5.
lo más grande posible. Por esta razón, cuando no se tiene conocimiento previo o una estimación de la proporción poblacional π, debemos utilizar π =0.5.
Esta segunda opción trae consigo varios inconvenientes como la posibilidad de sobreestimar el tamaño de la muestra necesario, lo que podría ocasionar un mayor costo en la realización del muestreo.
Finalmente el tamaño de la muestra puede ser calculado con la ecuación:
Veamos un ejemplo (cuando no conocemos el tamaño de la población):
¿A cuántas personas tendríamos que estudiar para conocer la prevalencia de los clientes de estratos 1, 2 y 3 en la empresa “El ejemplo S.A.S”?
Se ha establecido como parámetro que debe existir un nivel de confianza del 95% y un error de muestreo aceptable del 3%. Como no tenemos idea de dicha proporción porque ignoramos el tamaño real de la población, tendríamos que utilizar el valor p = 0,5 (50%) que maximiza el tamaño muestral:
En dicho caso, cuando se desconoce el volumen de la población, la muestra de mayor tamaño que la empresa “El ejemplo S.A.S” debe tomar es una de 203 clientes.