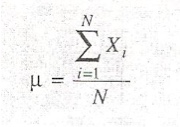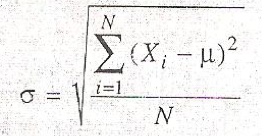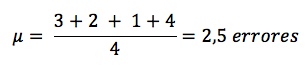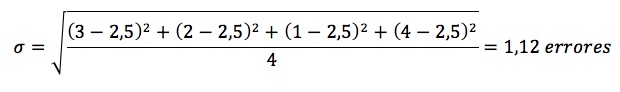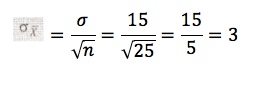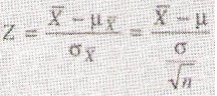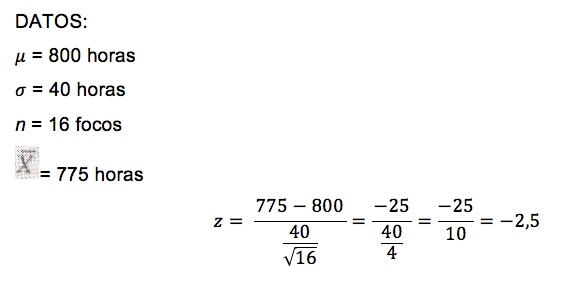Este artículo fue publicado hace más de un año, por lo que es importante prestar atención a la vigencia de sus referencias normativas.
La Norma Internacional de Auditoría –NIA– 530 que se refiere al muestreo, sugiere la importancia de las herramientas estadísticas para validar con mayor seguridad los datos sujetos a revisión. Este editorial presenta algunos elementos básicos de las distribuciones muestrales como herramienta para tal labor.
En algunas ocasiones, la labor del auditor requiere obtener conclusiones generales de casos particulares, lo que se traduce en la estadística inferencial como la utilización de estadísticos calculados a partir de muestras para estimar los valores de los parámetros de la población. Para el caso que nos interesa, vamos a centrarnos en la media muestral, una herramienta estadística utilizada para estimar la media poblacional (un parámetro).
Por ejemplo, al gerente de una empresa que comercializa bultos de papa le interesa utilizar la media muestral del peso de estos (ya que todos no van a ser iguales) calculada a partir de una muestra, para estimar el peso medio incluido en una población de bultos.
Hipotéticamente, al utilizar un estadístico muestral para estimar un parámetro poblacional, es necesario examinar toda posible muestra que pudiera presentarse. La distribución muestral es la distribución de los resultados que se presentan.
La media es la medición de la tendencia central que más se utiliza. La media muestral se utiliza para calcular la media poblacional. La distribución muestral de la media es la de todas las medias posibles que surgen si en realidad se llegaran a seleccionar todas las muestras posibles de cierto tamaño.
Esta propiedad se basa en que la media de todas las medias muestrales posibles (de una muestra dada con tamaño n) es igual a la media poblacional µ.
Podemos ejemplificar esta propiedad de la siguiente manera: se encuentra una población de cuatro asistentes administrativos. Se pide a cada uno de los asistentes que teclee la misma página de transacciones diarias en un software contable. La siguiente tabla muestra el número de errores.
|
Asistente administrativo |
Número de errores |
| Miguel |
X1 = 3 |
| María |
X2 = 2 |
| Esteban |
X3 = 1 |
| Sofía |
X4 = 4 |
Al obtener los datos de una población, la media se calcula utilizando la siguiente ecuación:
La media poblacional es la suma de los valores de la población dividida por el tamaño de la población N.
Luego se calcula la desviación estándar con la siguiente ecuación:
Ahora podemos resolver el problema de los asistentes administrativos:
La media muestral es un estimador imparcial de la media poblacional.
El error estándar de la media poblacional es igual a la desviación estándar de la población σ dividida por la raíz cuadrada del tamaño de la muestra n.
También es factible utilizar la anterior ecuación como aproximación del error estándar de la media cuando la muestra seleccionada sin reemplazo incluye menos de 5% de la población total.
Por ejemplo: Volvamos al proceso de la comercializadora de bultos de papa. Si de los miles de bultos de papa durante un turno se elige de manera aleatoria una muestra de 25 bultos sin reemplazo, la muestra contendrá mucho menos del 5% de la población. Suponiendo que la desviación estándar del peso de los bultos de papa es de 15 libras, es necesario calcular el error estándar de la media.
Solución: Al utilizar la ecuación presentada con anterioridad, con n=25 y σ =15, se determina que el error estándar de la media es:
Después de estudiar cómo obtener la media poblacional a través de la media muestral y el error estándar de la media, vamos a analizar la manera de obtener la probabilidad de error de un determinado valor en una distribución muestral.
Debemos encontrar la variable aleatoria continua Z, que es la diferencia entre la media muestral y la media poblacional, dividida por el error estándar de la media.
Por ejemplo: Una empresa eléctrica fabrica focos que tienen una duración estándar distribuida aproximadamente en forma normal, con media de 800 horas y desviación estándar de 40 horas. ¿Cuál es la probabilidad, en una muestra aleatoria, que 16 focos tengan una vida promedio de menos de 775 horas.
Procedemos a buscar en la tabla de distribución muestral de la media o distribución muestral normal, el valor obtenido de Z para saber su equivalencia en probabilidad:
En este caso e valor obtenido fue -2,5 y su equivalencia es 0,0062; por tanto, existe una probabilidad de 0,62% a que la media muestral de 16 focos sea menor a 775 horas.
Fundada en el año 2000 con la misión de “elevar el nivel profesional del Contador Público”
